Subdivisions et fonctions en escalier.
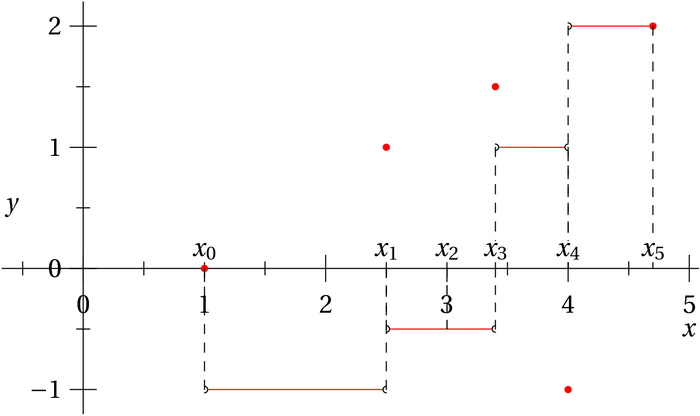
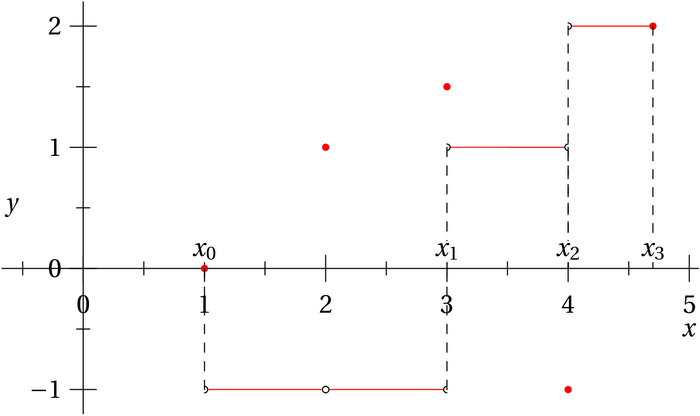
Commençons par un premier exemple, la fonction en escalier et une subdivision adaptée
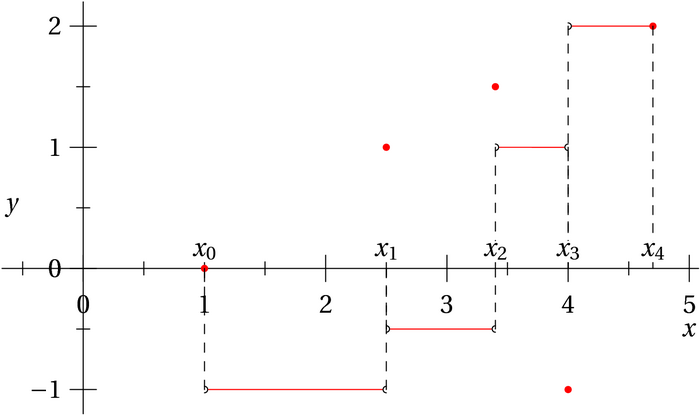
Ci-dessous, la subdivision “minimale” de la fonction en escalier
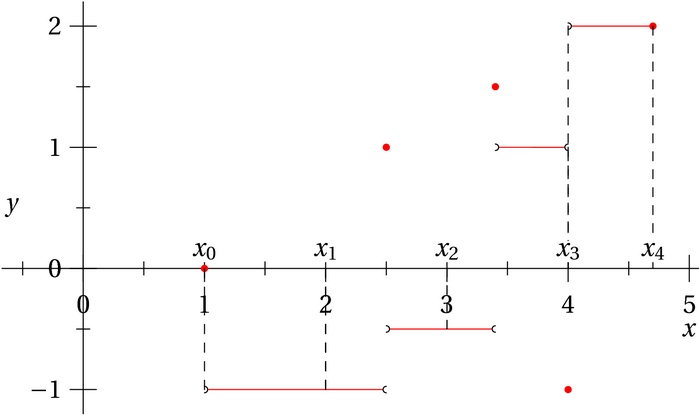
Ci-dessous, toujours notre fonction et une subdivision qui n’est pas adaptée !
Question. Dans le dessin ci-dessous, la subdivision est-elle adaptée ?
Produits, somme, valeur absolue de fonctions en escalier.
Clairement tout le monde a compris !
Intégrale d’une fonction en escalier
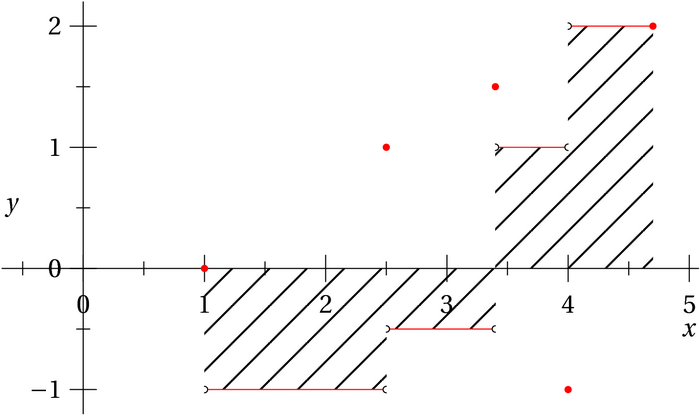
D’après le cours, l’intégrale de notre fonction en escalier fétiche est représentée par l’aire algébrique correspondant aux hachures.
Il faut bien comprendre que si une fonction positive en escalier est petite alors son intégrale est petite, mais si l’intégrale d’une fonction en escalier est petite celle-ci n’est pas nécessairement petite:
Encadrement d’une fonction gentille par deux fonctions en escalier
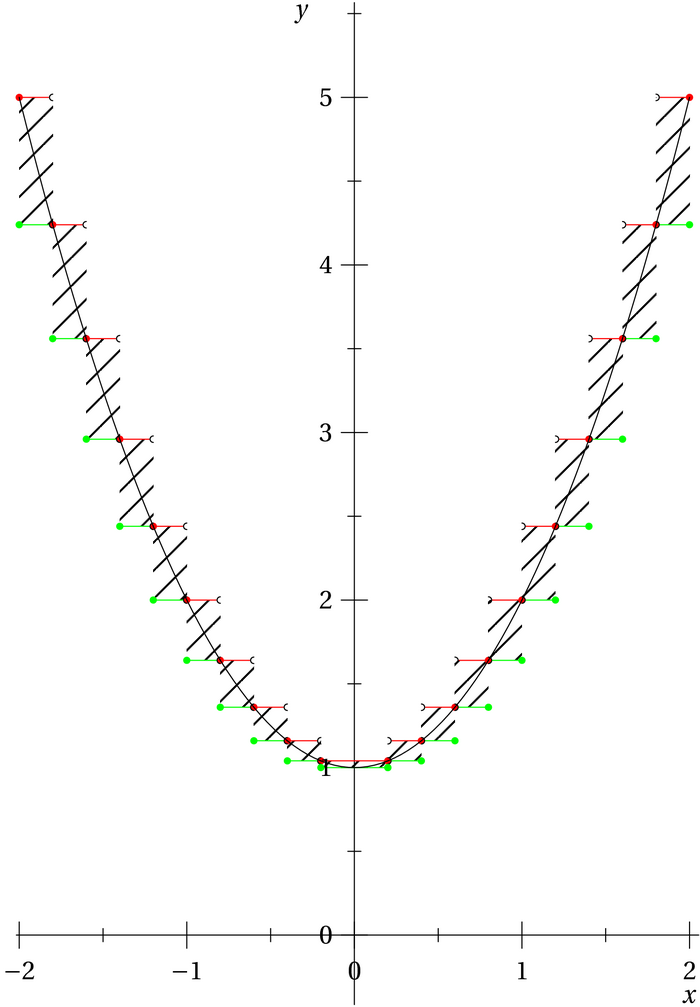
Ci-dessous on a le graphe de la fonction \(f(x)=1+x^2\), celui de deux fonctions en escalier qui encadrent \(f\). L’aire hachurée correspond à \(\int_{-2}^{2}{\psi-\varphi dx}\) qui doit être petite. Le graphique en dessous correspond effectivement à la fonction étagée \(\psi-\varphi\).
Si on diminue le pas de la subdivision équidistante on voit de moins en moins les détails (ici la zone n’est pas hachurée mais colorée) :
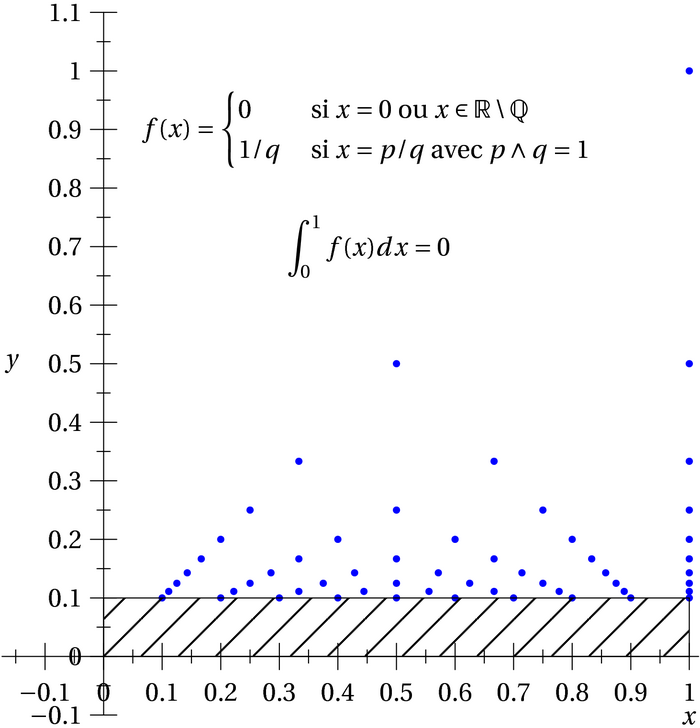
Une fonction qui fait peur mais qui est intégrable au sens de Riemann
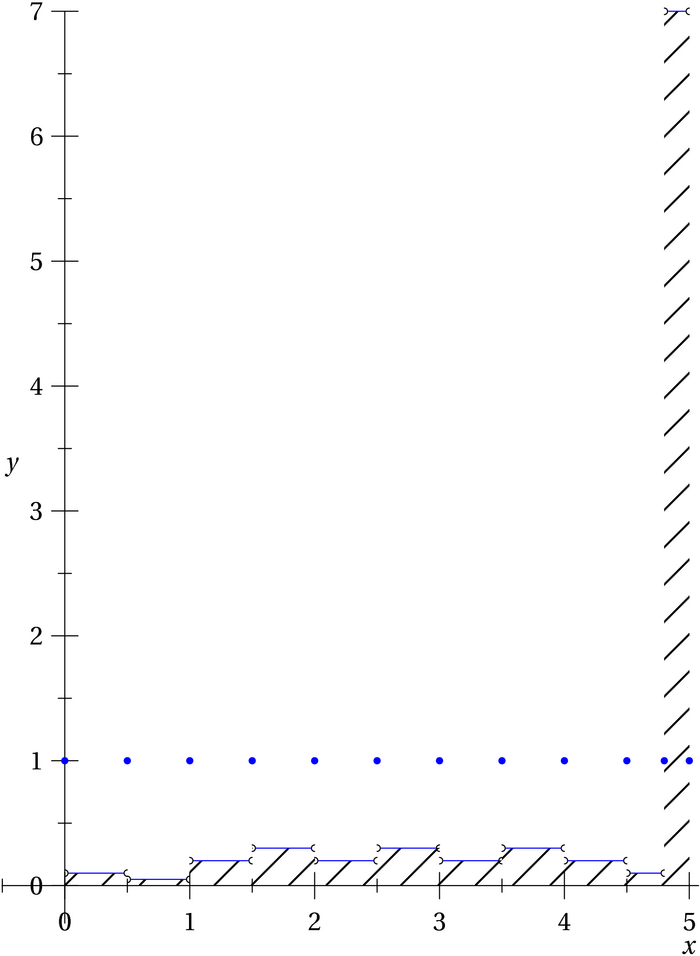
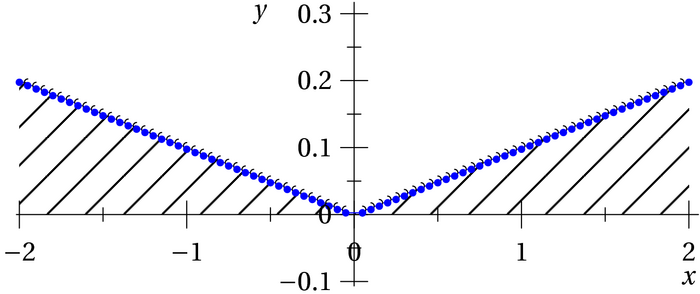
Dans le graphique ci-dessous, les points bleus correspondent aux seules
valeurs de la fonctions qui sont plus grandes que 1/10 ! Partout
ailleurs cette fonction prend des valeurs strictement plus petites que
1/10. Il faut imaginer que pour un entier naturel \(n\)
quelconque et grand la situation est similaire, à savoir qu’il y a un
nombre fini de points où la fonction prend une valeur supérieure ou
égale à \(1/n\). Par contre je ne peux pas tracer la
fonction qui fait peur et qui n’est pas intégrable au sens de Riemann
!