Problème raide

Grosso modo, une équation différentielle ordinaire est dite raide si les méthodes numériques usuelles nécessitent un pas anormalement petit.

Modèle de Robertson

En cinétique chimie, il arrive qu'une équation bilan soit en réalité un mécanisme plus complexe avec plusieurs réactions chimiques en parallèles mais avec des vitesses très différentes (l'oxydation du sulfite de cuivre par exemple).

Le modèle de Robertson : 3 quantités chimiques \(A\), \(B\) et \(C\) et une équation bilan

\[A \longrightarrow B \quad \text{lente $k_1=0.04$}\]\[B + B \longrightarrow C + B \quad \text{très rapide $k_2=3.10^7$}\]\[B + C \longrightarrow A + C \quad \text{rapide $k_3=10^4$}\]

Le modèle (suite)

Si \(y_a,y_b,y_c\) désignent respectivement les concentrations des quantités \(A,B,C\) alors les lois de la cinétique chimie donnent

\[y'_a(t)=-k_1y_a(t)+k_3 y_b(t)y_c(t)\]\[y'_b(t)=k_1 y_a(t)-k_3y_b(t)y_c(t)-k_2(y_b(t))^2\]\[y'_c(t)=k_2(y_b(t))^2\]

avec les conditions initiales \(y_a(0)=1, y_b(0)=0, y_c(0)=0\).

Avec Python -1-

Avec les routines écrites il suffit de définir \(F(t,x)\) à valeurs vectorielles.

def f(t,x):
    k1, k2, k3 = 0.04, 3*10**7, 10**4
    return np.array([-k1*x[0]+k3*x[1]*x[2], k1*x[0]-k3*x[1]*x[2]
             -k2*x[1]**2,k2*x[1]**2])

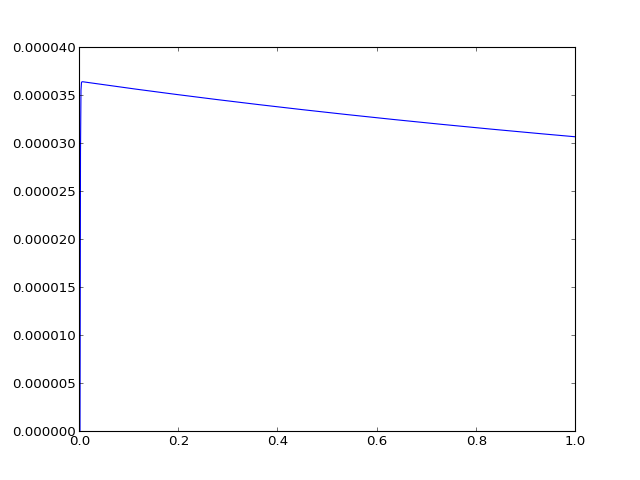
Euler : N=300, T=.3. Visualisons \(y_b\)

(Source code)

_images/raide1.png

Suite avec Runge-Kutta d'ordre 4

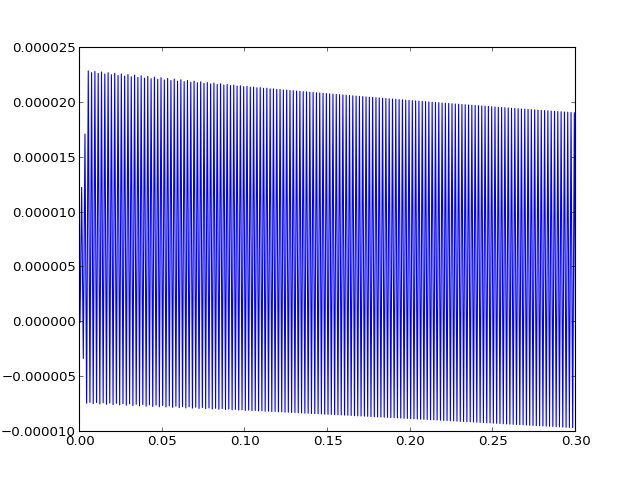
Runge-Kutta d'ordre 4 : N=300, T=.5. Visualisons \(y_b\)

(Source code)

_images/raide2.png

Euler implicite

\[y_{n+1}=y_n+hf(t_{n+1},y_{n+1})\]

donnera de meilleurs résultats. C'est un schéma d'ordre 1 alors que celui Runge-Kutta utilisé ici est d'ordre 4. Implémenter un schéma implicite nécessite à chaque pas de résoudre une équation non-linéaire, ce qui peut être délicat. Avec la fonction fsolve de Scipy on modifie le schéma d'Euler explicite en

from scipy.optimize import fsolve
# on importe juste la routine fsolve
for i in range(n):
        j=i
        ti=tpt[i+1]
        y=Y[:,i]
        def G(x):  # la fonction dont il faut trouver le zéro
            return y+dt*f(ti,x)-x
        ti=tpt[i+1]
        Y[:,i+1]=fsolve(G,Y[:,i])

Euler implicite

Euler implicite : N=300, T=.3. Visualisons \(y_b\)

(Source code)

_images/raide3.png

Avec Python et Scipy -2-

Scipy possède plusieurs solveurs d'EDO.

Limitons nous à odeint. Cette fonction possède de nombreux paramètres dont les valeurs par défaut sont définies (heureusement), comme le pas, la tolérance, etc. Nous utiliserons simplement la syntaxe

odeint(f,y0,t)

où t est un vecteur (array) dont la première valeur est \(t_0\) le temps initiale. La fonction retourne sous forme d'un vecteur les approximations de la solution en les valeurs de t.

Suite

Dans notre cas, c'est très simple sauf que la fonction \(f\) doit être de la forme f(x,t) et non pas f(t,x) !

In [1]: import numpy as np

In [2]: from scipy.integrate import odeint

In [3]: def f(x,t):
   ...:   k1, k2, k3 =0.04, 3*10**7, 10**4
   ...:   return np.array([-k1*x[0]+k3*x[1]*x[2], k1*x[0]-k3*x[1]*x[2]-k2*x[1]**2,
   ...:       k2*x[1]**2])
   ...: 

In [4]: y0=np.array([1. ,0., 0.])

In [5]: t=np.array([0., .3])

In [6]: print (odeint(f,y0,t))
[[  1.00000000e+00   0.00000000e+00   0.00000000e+00]
 [  9.88673942e-01   3.44771582e-05   1.12915812e-02]]

Raide ou pas

In [2]: from scipy.integrate import odeint

In [4]: y0=np.array([1. ,0., 0.])

In [5]: t=np.array([0., .1, .2, .3])

In [6]: print (odeint(f,y0,t,full_output=True)[1])
{'nfe': array([84, 95, 96], dtype=int32), 'nje': array([4, 5, 5], dtype=int32), 'tolsf': array([ 0.,  0.,  0.]), 'nqu': array([3, 4, 4], dtype=int32), 'lenrw': 68, 'tcur': array([ 0.10335521,  0.25509646,  0.32184304]), 'hu': array([ 0.02833156,  0.06674658,  0.06674658]), 'imxer': -1, 'leniw': 23, 'tsw': array([ 0.00551435,  0.00551435,  0.00551435]), 'message': 'Integration successful.', 'nst': array([40, 44, 45], dtype=int32), 'mused': array([2, 2, 2], dtype=int32)}

In [7]: print (odeint(f,y0,t,full_output=True)[1]['mused'])  #méthode utilisée
[2 2 2]

2 veut dire raide ou stiff et dans ce cas odeint utilise une méthode adéquate, BDF (backward differentiation formula), bref de l'implicite.

Un dernier graphique

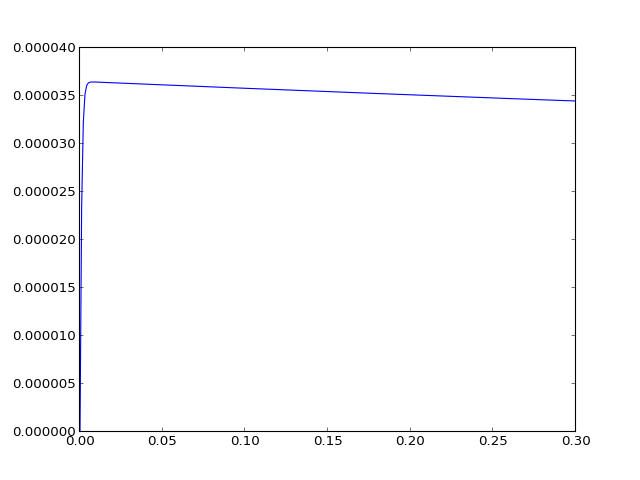
Y=odeint(f,y0,tpt)
plt.plot(tpt,Y[:,1])  # on trace la concentration de B

(Source code)

_images/raide5.png