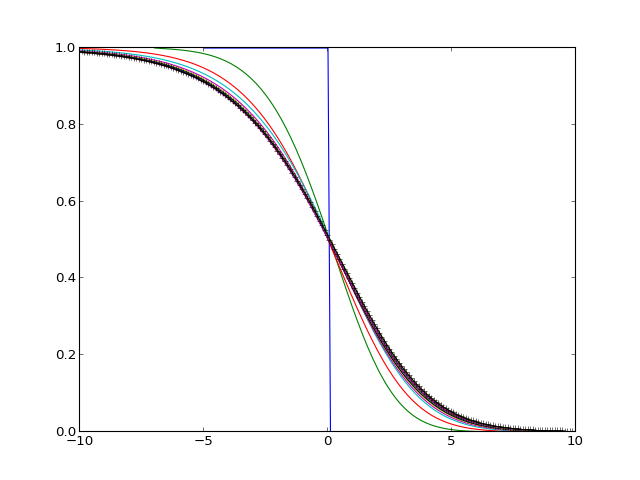
Équation de Fisher

C'est un modèle d'évolution de population (évolution d'un gène dominant), un cas particulier des équation KPP (Kolmogorov-Petrovsky-Piskounov) :

\[\frac{\partial u}{\partial t} - \frac{\partial^2 u}{\partial x^2}= u(1-u) \qquad (t,x)\in\mathbb{R}^+\times\mathbb{R}\]

Propriétés : existence de front d'ondes stationnaires

Onde stationnaire

Une onde stationnaire se déplaçant à la vitesse \(c\) est une solution particulière de la forme \(u(t,x)=U(x-ct)\). En posant \(z=x-ct\), \(U\) vérifie une équation différentielle ordinaire

\[U''+cU'+U(1-U)=0\]

On s'intéresse aux ondes stationnaires qui opèrent une transition entre les deux états d'équilibre \(U=1\) et \(U=0\) et vérifiant \(0\leq U\leq 1\).

On démontre que pour tout \(c\geq 2\) il existe une unique onde stationnaire se déplaçant à la vitesse \(c\). Pour \(c<2\) une telle onde n'existe pas.

Construction numérique : en raccordant les solutions des linéarisées autour des deux points d'équilibres et bien sûr odeint (à faire)

Propriété

Kolmogorov, Petrovskii et Piscounov (1937) ont démontré que pour toute donnée unitiale \(u_0\) vérifiant

\[u_0(x)=1 \quad\forall x\leq x_1, \qquad u_0(x)=1 \quad\forall x\geq x_2\]\[0\leq u_0(x)\leq 1\]

alors la solution \(u(x,t)\) converge quant \(t\) tend vers l'infini vers une onde stationnaire se déplaçant à la vitesse \(c=2\).

Avec Python, Numpy et Matplotlib

schémas explicite, implicite
mise en évidence de l'instabilité du schéma explicite
effet régularisant du à la présence de \(u_{xx}\)
évolution vers une onde stationnaire se déplaçant à la vitesse 2

Différences finies

On utilise les formules

\[\frac{\partial u}{\partial t}(t,x) \approx \frac{u(t+k,x)-u(t,x)}{k} \quad\text{progressive}\]\[\frac{\partial u}{\partial t}(t,x) \approx \frac{u(t,x)-u(t-k,x)}{k} \quad\text{retrograde}\]\[\frac{\partial^2 u}{\partial^2 x}(t,x)\approx \frac{u(t,x+h)-2 u(t,x)+ u(t,x-h)}{h^2}\]

On discrétise alors \([0,T]\times[-a,a]\) et non pas \(\mathbb{R}^+\times\mathbb{R}\) :

\[k=\Delta t= \frac{T}{M+1}, \quad h=\Delta x=\frac{2a}{N+1}\]\[t_{j}=jk \quad 0\leq j\leq M+1, \qquad x_{n}=a+nh\quad 0\leq n\leq N+1\]

Différences finies (suite)

On pose \(U_{j,n}\) avec \(0\leq j\leq M+1\) et \(0\leq n\leq N+1\) sensé être une approximation de \(u(t_j,x_n)\). Écrire l'EDP en \((t_j,x_n)\) avec les formules donnent plusieurs schémas (il y a plusieurs choix possibles entre la différence progressive, rétrograde ou une moyenne des deux) : explicite et implicite

\[\dfrac{U_{j+1,n}-U_{j,n}}{k} -\dfrac{U_{j,n+1}-2U_{j,n}+U_{j,n-1}}{h^{2}}= U_{j,n}(1-U_{j,n})\]\[\dfrac{U_{j,n}-U_{j-1,n}}{k} -\dfrac{U_{j,n+1}-2U_{j,n}+U_{j,n-1}}{h^{2}}= U_{j-1,n}(1-U_{j-1,n}).\]

Pour éviter d'avoir une équation non linéaire à résoudre dans le schéma implicite, le second membre est évalué en \(t_{j-1},x_n\).

Il faut pour boucler le système (et même l'EDP sur le domaine borné) ajouter des conditions sur le bord. Pour faire simple nous prendrons Dirichlet non homogène \(u(t,-a)=1\) et \(u(t,a)=0\), en accord avec le théorème.

Matrice du problème de Dirichlet

La matrice \(A\) utilisée dans la suite appelée matrice de Dirichlet :

\[\begin{split}\begin{pmatrix} 2 & -1 &\; &\; &\; \cr -1 &2 &-1 &\; &\; \cr \: &\ddots &\ddots &\ddots &\; \cr \: & \: &\ddots &\ddots & -1 \cr \; &\; & \: &-1 &2 \cr \end{pmatrix}\end{split}\]

Différences finies (forme matricielle)

Si \(U^{(j)}\) désigne le vecteur de taille \(N\) contenant \(U_{j,n}\) pour \(1\leq n\leq N\) on peut écrire les deux schémas sous forme matricielle

\[U^{(j+1)}=(I-\frac{k}{h^2}A)U^{(j)}+ k F^{(j)}\]\[\big(I+\frac{k}{h^{2}}A\big) U^{(j+1)}=U^{(j)} + k F^{(j)}\]

avec \(F^{j}_n= U_{j,n}(1-U_{j,n})\) si \(2\leq n\neq N\) et \(F^j_1= \frac{1}{h^2}+ U_{1,n}(1-U_{1,n})\)

Comme nous avons un problème d'évolution, la donnée initiale \(u_0\) initialise \(U^{(0)}\) avec \(U_{0,n}=u_0(x_n)\) : le premier schéma est dit explicite et le second implicite (à chaque étape on doit résoudre un système linéaire).

Consistance, stabilité et convergence

Comme pour les EDO on définit les notions de consistance, de stabilité et de convergence.

Le schéma explicite souffre d'un gros défaut : il est stable si et seulement si \(k\leq 2\) (\(k\) a vocation à devenir petit) et

\[\frac{k}{h^2} \leq \frac{1}{2}- \frac{k}{4}\]

Si le second membre de l'EDP est une donnée \(f\) (qui ne dépend pas de \(u\)) on a la condition CFL usuelle \(k/h^2\leq 1/2\). On demande donc un pas de temps très petit devant le pas d'espace.

Le schéma implicite est inconditionnellement stable (sous réserve ici d'avoir \(k<2\), ce qui est raisonnable).

Schéma explicite

Le code avec les créations de matrices particulières de Numpy

def schem_expl(y0,T,a,M,N):
    dx, dt = 2*a/(N+1), T/(M+1)
    A=2*np.diag(np.ones(N))-np.diag(np.ones(N-1),-1)-np.diag(np.ones(N-1),1)
    G=np.eye(N)-dt/(dx**2)*A
    Y=np.zeros((M+2,N+2))
    tpt=np.linspace(0,T,M+2)
    xpt=np.linspace(-a,a,N+2)
    Y[0,:]=y0(xpt)
    Y[:,0]=1
    F=np.zeros(N)
    for i in range(M+1):
        F=Y[i,1:-1]*(1-Y[i,1:-1])
        F[0]=F[0]+1/(dx**2)
        Y[i+1,1:-1]=np.dot(G,Y[i,1:-1])+dt*F
    return tpt, xpt, Y

Schéma explicite : stabilité ?

schem_expl(y1,10,10,10000,500) (donne l'erreur overflow ...) avec donnée initiale discontinue 1 sur \(]-\infty,-4[\) et 0 ailleurs.

(Source code)

Schéma explicite : stabilité ?

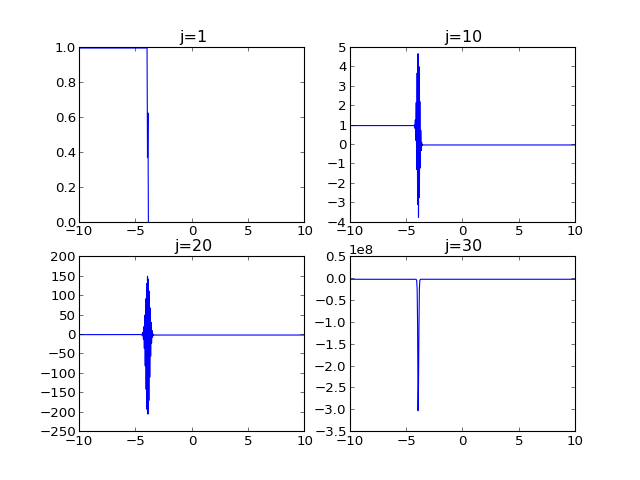
schem_expl(y1,10,10,10000,200) avec un tracé sur une sélection de temps. Vers la fin, la progression de l'onde et la condition au limite imposée en \(a\) ne sont plus valides du point de vue du modèle.

(Source code)

Schéma implicite

Il suffit d'ajouter

from numpy.linalg import solve

def schem_impl(y0,T,a,M,N):
    dx, dt = 2*a/(N+1), T/(M+1)
    A=2*np.diag(np.ones(N))-np.diag(np.ones(N-1),-1)-np.diag(np.ones(N-1),1)
    G=np.eye(N)+dt/(dx**2)*A
    Y=np.zeros((M+2,N+2))
    tpt=np.linspace(0,T,M+2)
    xpt=np.linspace(-a,a,N+2)
    Y[0,:]=y0(xpt)
    Y[:,0]=1
    F=np.zeros(N)
    for i in range(M+1):
        F=Y[i,1:-1]*(1-Y[i,1:-1])
        F[0]=F[0]+1/(dx**2)
        Y[i+1,1:-1]=solve(G, Y[i,1:-1]+dt*F)  # résolution du système linéaire
    return tpt, xpt, Y

Schéma implicite : stabilité ?

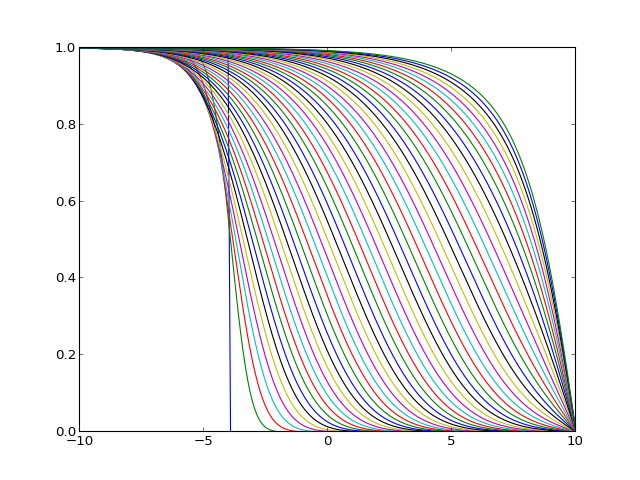
schem_impl(y1,8,10,100,800) donne

(Source code)

Saisir l'onde stationnaire

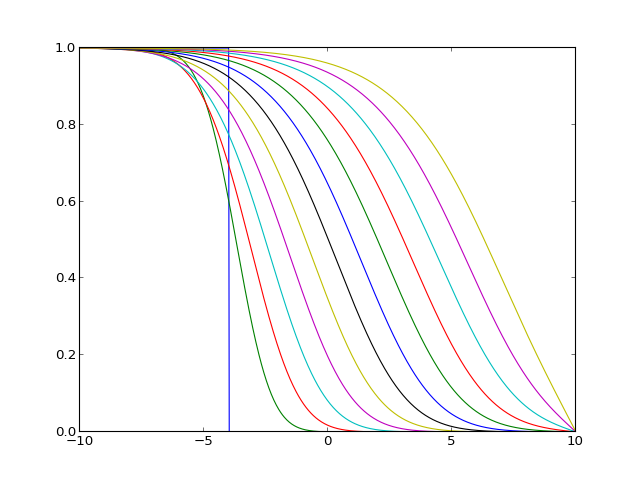
À l'aide du schéma implicite, pour visualiser la forme de l'onde :

schéma implicite
fenêtre suffisamment large par rapport au temps final de la simulation
recentrage de la solution

def y1(x):
         return np.ones(np.size(x))*[x<-7]

tpt, xpt, Y = schem_impl(y1,8,10,1000,800)
plt.axes(xlim=(-10,10),ylim=(0,1))
for i in range(0,tpt.size):
         if i%80==0:
              n=np.max(np.nonzero(Y[i,:]>=0.5))
         xd=xpt[n]
         plt.plot(xpt-xd,Y[i,:])
plt.show()

Onde stationnaire

tpt, xpt, Y = schem_impl(y1,8,10,1000,800)

(Source code)

Onde stationnaire

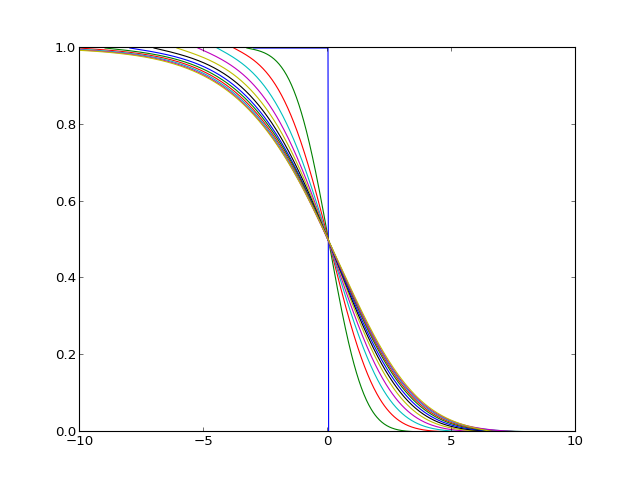
tpt, xpt, Y = schem_impl(y1,30,40,10000,800) sur la fenêtre \([-10,10]\) et tracé de l'approximation en \(T=20\) :

(Source code)

Exercices

tracé d'une onde stationnaire par l'EDO en fonction de la vitesse
superposition du tracé de l'onde stationnaire calculée pour \(c=2\) et de l'approximation de l'EDP recentrée
étude de la stabilité de l'onde stationnaire
schéma de Crank-Nicholson
condition de Neumann sur le bord