Un modèle simple de corde élastique

Le modèle consiste en une chaîne de ressorts de même caractéristique et supposés idéaux (loi de Hooke).

Le système différentiel

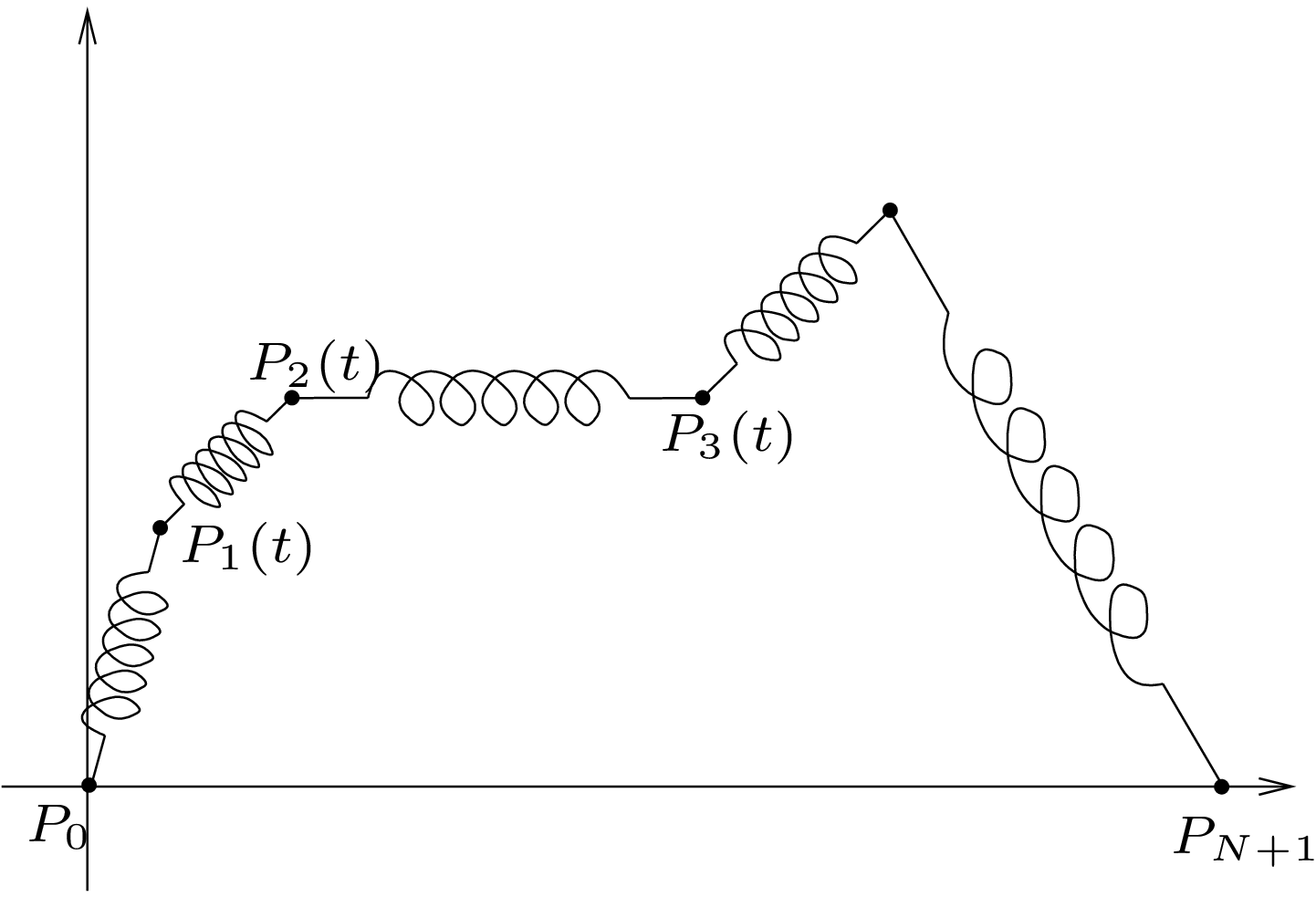
La chaîne est dans un plan. Les deux extrémités de la chaîne sont fixées à une même hauteur. On dispose de \(N+1\) ressorts donc \(N+2\) points. La loi de Hooke nous donne une équation différentielle d'ordre 2 pour les \(N\) points intérieurs. Chaque point ayant deux coordonnées on obtient un système différentiel du 1er ordre de dimension \(4*N\).

_images/figcorde.png

Le système différentiel

Loi de Hook : force dirigéee vers l'intérieur en compression et l'extérieur en extension de norme égale à

\[|f| =k \frac{\vert l-l_0\vert }{l_0}\]

où \(l_0\) est la longueur du ressort au repos et \(k\) la constante de raideur au repos.

Hypothèse idéale : loi reste vraie pour toute valeur de \(l\).

La masse \(i\) est soumise à l'action de deux forces, \(f_{i,i-1}\) et \(f_{i,i+1}\). Donc

\[m \frac{d^2P_i}{dt^2}=f_{i,i-1}+f_{i,i+1}\quad 1\leq i\leq N.\]

Suite

et la loi de Hook donne

\[ f_{i,i-1}=k\bigg(\frac{\|P_i(t)-P_{i-1}(t)\|}{l_0}-1\bigg) \frac{ P_{i-1}(t)-P_i(t)}{\|P_i(t)-P_{i-1}(t)\|},\]\[f_{i,i+1}=k\bigg(\frac{\|P_i(t)-P_{i+1}(t)\|}{l_0}-1\bigg) \frac{ P_{i+1}(t)-P_i(t)}{\|P_i(t)-P_{i+1}(t)\|}.\]

En posant \(P_i(t)=(Y_{1,i}(t),Y_{2,i}(t))\), \(P_i'(t)=(Y_{3,i}(t),Y_{4,i}(t))\) on se ramène à un système de taille \(4N\)

Le système (enfin)

\[{}\small \frac{dY}{dt}(t)=F(Y)\]\[{}\small F(Y)_{1,i}=Y_{3,i},\quad F(Y)_{2,i}=Y_{4,i}\]

Puis les 3ème et 4ème coordonnées

\[{}\small \frac{k}{ml_0}\Big[ \big(1-\frac{l_0}{\eta_i^-(Y)}\big) (Y_{1,i-1}-Y_{1,i}) + \big(1-\frac{l_0}{\eta_i^+(Y)}\big) (Y_{1,i+1}-Y_{1,i})\Big]\]\[{}\small \frac{k}{ml_0}\Big[ \big(1-\frac{l_0}{\eta_i^-(Y)}\big) (Y_{2,i-1}-Y_{2,i}) + \big(1-\frac{l_0}{\eta_i^+(Y)}\big) (Y_{2,i+1}-Y_{2,i})\Big]\]\[{}\small \eta_i^\pm(Y)=\sqrt{(Y_{1,i\pm 1}-Y_{1,i})^2+(Y_{2,i\pm 1}-Y_{2,i})^2}\]

Avec Python

Au pire

\[{}\small \frac{k}{ml_0}\Big[ \big(1-\frac{l_0}{\eta_i^-(Y)}\big) (Y_{1,i-1}-Y_{1,i}) + \big(1-\frac{l_0}{\eta_i^+(Y)}\big) (Y_{1,i+1}-Y_{1,i})\Big]\]\[{}\small \frac{k}{ml_0}\Big[ \big(1-\frac{l_0}{\eta_i^-(Y)}\big) (Y_{2,i-1}-Y_{2,i}) + \big(1-\frac{l_0}{\eta_i^+(Y)}\big) (Y_{2,i+1}-Y_{2,i})\Big]\]\[{}\small \eta_i^\pm(Y)=\sqrt{(Y_{1,i\pm 1}-Y_{1,i})^2+(Y_{2,i\pm 1}-Y_{2,i})^2}\]

pourrait se faire avec une boucle mais le programme sera lent pour \(N\) grand.

Éléments du programme

Pour le calcul de \(F\) la vectorisation Numpy

def fressort(Y):
    global k,m,l0,e
    Z=np.zeros_like(Y)
    Z[0,:]=Y[2,:]
    Z[1,:]=Y[3,:]
    Ye=np.hstack((np.zeros((4,1)),Y,np.zeros((4,1))))
    Ye[0,-1]=1
    etap=np.sqrt((Ye[0,2:]-Y[0,:])**2+(Ye[1,2:]-Y[1,:])**2)
    etam=np.sqrt((Ye[0,:-2]-Y[0,:])**2+(Ye[1,:-2]-Y[1,:])**2)
    Z[2,:]=k/(m*l0)*((1-l0/etam)*(Ye[0,:-2]-Y[0,:])+(1-l0/etap)*(((Ye[0,2:]-Y[0,:]))))
    Z[3,:]=k/(m*l0)*((1-l0/etam)*(Ye[1,:-2]-Y[1,:])+(1-l0/etap)*(((Ye[1,2:]-Y[1,:]))))
    return Z

Éléments du programme

Un Runge-Kutta spécifique qui retourne la suite des valeurs \(Y_{1,i},Y_{2,i}\) toutes les 16 itérations

def myrk4(f,t0,T,y0,n):
    dt, Y = T/n, y0
    SYx=np.zeros((1+(n+1)//16,y0.shape[1]+2))
    SYx[:,-1]=1
    SYy=np.zeros((1+(n+1)//16,y0.shape[1]+2))
    SYx[0,1:-1] , SYy[0,1:-1] = y0[0,:] , y0[1,:]
    for i in range(n):
        p1=f(Y)
        Y2=Y+dt/2*p1
        p2=f(Y2)
        Y3=Y+dt/2*p2
        p3=f(Y3)
        Y4=Y+dt*p3
        p4=f(Y4)
        Y=Y+dt*(p1+2*p2+2*p3+p4)/6
        if (i+1)%16==0:
            SYx[(i+1)//16,1:-1]=Y[0]
            SYy[(i+1)//16,1:-1]=Y[1]
    return SYx,SYy

Un exemple

(Source code)

_images/corde-1.png

Animation

Suite des expériences