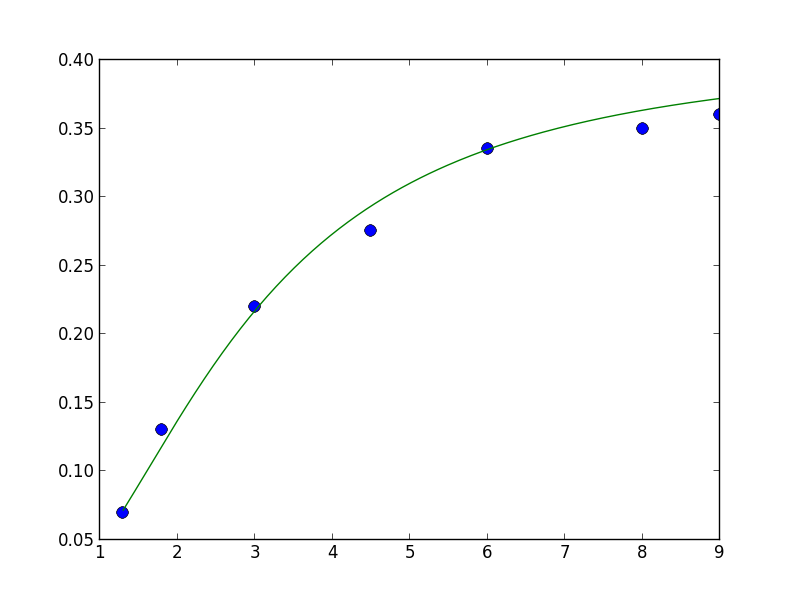
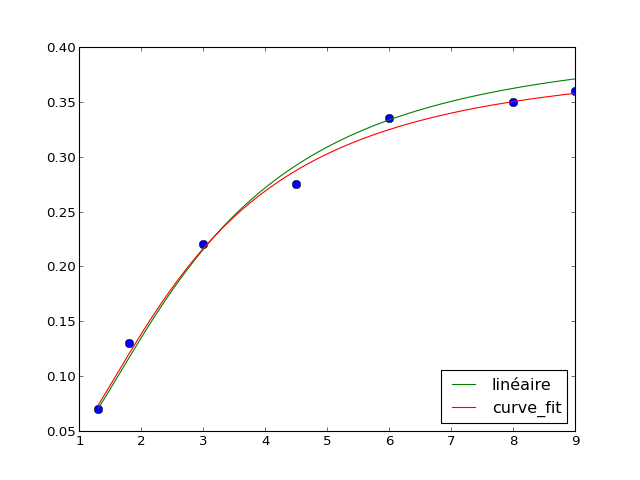
Ajustement de courbe

Pour des données expérimentales ou non, on cherche à ajuster des paramètres d'une classe de fonctions définies pour approcher au mieux la courbe expérimentale. Bien souvent la classe de fonction est l'ensemble des polynômes (de degré maximum fixé), de polynômes trigonométrique et on tombe sur la classique régression linéaire. Le "au mieux" dépend aussi de la façon dont on mesure la distance entre courbe expérimentale et classe de fonctions.

Loi de Michaelis-Menten (ou Hill)

Dans le cadre de réactions enzymatiques, on propose le modèle

\[v=\frac{ v_{m} [S]^{2}}{k_{s}^{2}+[S]^{2}},\]

où \(v\) est la vitesse initiale de réaction, \(v_{m}\) la vitesse initiale maximale mesurée pour une concentration saturante de substrat, \(k_{s}\) la constante de mi-saturation et \([S]\) la concentration en substrat.

Le but est, par une méthode de moindres carrés, d'estimer les paramètres \(v_{m}\) et \(k_s\) d'après la série suivante de mesures de \(v\) et \([S]\)

[S] 1.3 1.8 3 4.5 6 8 9
v 0.07 0.13 0.22 0.275 0.335 0.35 0.36

Loi linéaire à un changement de variable près

\[v=\frac{ v_{m} [S]^{2}}{k_{s}^{2}+[S]^{2}}\]

en changeant les variables devient linéaire

\[\frac{1}{v}=\frac{k_{s}^{2}}{v_{m}} \frac{1}{[S]^{2}}+ \frac{1}{v_{m}}.\]

Il suffit donc d'une classique régression linéaire pour "ajuster au mieux" les paramètres cherchés.

Il suffit de construire la matrice \(A\) de taille (7,2) et le second membre

Avec Numpy

In [3]: d=np.array([ 1.3 , 1.8 , 3   , 4.5 , 6   , 8   ,9])

In [4]: A=np.vstack((d*d, np.ones(7)))

In [5]: A=1/A.transpose()

In [6]: A
Out[6]: 
array([[ 0.59171598,  1.        ],
       [ 0.30864198,  1.        ],
       [ 0.11111111,  1.        ],
       [ 0.04938272,  1.        ],
       [ 0.02777778,  1.        ],
       [ 0.015625  ,  1.        ],
       [ 0.01234568,  1.        ]])

In [7]: b=np.array([ 0.07, 0.13 , 0.22 , 0.275 , 0.335 , 0.35 ,0.36])

In [8]: np.linalg.lstsq(A,1/b)
Out[8]: 
(array([ 19.37599713,   2.4492275 ]),
 array([ 0.75664547]),
 2,
 array([ 2.68056384,  0.52527866]))

Avec Numpy et Matplotlib

In [1]: x=np.linalg.lstsq(A,1/b)[0]

In [2]: vm, km =1/x[1], (x[0]/x[1])**.5

In [3]: print(vm,km)
0.408292003061 2.81266149359

In [4]: xpt = np.linspace(1.3,9,200)

In [5]: plt.plot(d,b,'o',markersize=8,linewidth=4);

In [6]: plt.plot(xpt, vm*xpt**2/(km**2+xpt**2));
_images/fitting0.png

Avec Scipy et Matplotlib

Scipy possède une routine de moindres carrés non linéaires : curve_fit. La documentation dit

import numpy as np
from scipy.optimize import curve_fit
def func(x, a, b, c):
    return a*np.exp(-b*x) + c
x = np.linspace(0,4,50)
y = func(x, 2.5, 1.3, 0.5)
yn = y + 0.2*np.random.normal(size=len(x))
popt, pcov = curve_fit(func, x, yn)

In [2]: def f(x,a,b):
   ...:      return a*x**2/(b**2+x**2)
   ...: 

In [3]: popt, pcov = curve_fit(f,d,b)

In [4]: print (popt)
[ 0.39030659  2.66739625]

Les deux solutions

Comme la quantité est différente selon la méthode utilisée, les deux résultats sont différents

(Source code)

_images/fitting1.png